WIIW The Vienna Institute for International Economic Studies - Wiener Institut für Internationale Wirtschaftsvergleiche

'If you are not willing to even consider a clash, you’re not negotiating.' - Yanis Varoufakis

'I am not ready to make nice, I am not ready to back down.' - Dixie Chicks

What is the payoff structure in the Greece versus Euro Area (EA) game? Games are defined by payoffs. No payoffs, no game. As we do not know the payoff structure, we need to infer it from the strategy of the players. One possibility is this: Greece expects the best result if it does not cooperate and the EA cooperates. If both do not cooperate, that is the worst outcome for Greece, because it is committed to staying in the monetary union and the EU (the new government does not have mandate to leave either of them) – and those are cooperative structures. The EA does better if cooperating than if not cooperating, but its worst outcome is if it cooperates while Greece does not. The EA gets its third best outcome, while Greece its worst, if failure to cooperate is the outcome of the game. For Greece, lack of cooperation being the strategy, failure to agree is better than cooperating on EA uncooperative terms. The game differs from prisoners’ dilemma (PD): in the PD joint uncooperative solution would be the third best for both, while the cooperative solution would be the second best, as here.

Greece-EA game (1 best, 4 worst; x, y, z, w are alternatives)

Not cooperating for EA means sticking to the existing Troika programme; for Greece it means scrapping the Troika programme; cooperating for EA means postponing and rescheduling the Troika programme; for Greece, cooperating means renegotiating a new programme with the EA, the EU, the ECB, and the IMF separately. The game as defined by this pay-off structure has one pure strategy Nash equilibrium (2, 2, or alternative y) and no mixed strategy Nash equilibrium.

How could the game be played? The dominant strategy for EA is not to cooperate. With that, Greece is better off cooperating rather than not cooperating. Greece, indeed, would want eventually to get to the cooperative outcome. That is the weakness in its position, as the interest in eventually cooperating is not enough to move the EA to be cooperative. Because, if Greece were rational, once EA declares its willingness to cooperate, Greece does better by not cooperating. So, assuming both players are rational, EA sticks to the strategy of not cooperating and waits for Greece to give up or shoot itself in the foot.

So, Greece signals that it is irrational. It is preferring clash over cooperation. That could work in the following way. Greece succeeds in being convincing as an irrational player: e.g. people are on the streets, the prime minister mobilises the support of the parliament, the finance minister declines all offers in negotiations. It will go, it is irrevocably committed to go, for the worst outcome rather than cooperate with the uncooperative EA, but it will also cooperate if EA cooperates. Why? Because it is consistently irrational, and being irrational it will cooperate, even though it is better, rationally, for Greece not to cooperate when EA is cooperative.

So, Greece needs to project the image of rather thorough irrationality, not of cleverness or cunningness. Not to be intransigent only as long as the other player is not ready to cooperate and then, when EA is ready to cooperate, switch back to the rational choice of not cooperating. It needs to play the uncooperative move until the EA decides to cooperate, then it indeed should cooperate, even though that is the inferior move in this game, at that point.

That is the best that the rational EA can get by playing with the irrational Greece and vice versa. The result is the Nash equilibrium.

Decision making rules (P=strict preference; R=preference. i.e. at least as good as; I=clash or joint indifference):

Expected payoff for both players: 2 (Nash equilibrium in pure strategies: Greece does not cooperate if EA does not cooperate, but cooperates if EA cooperates; EA does not cooperate if Greece does not, but cooperates if Greece cooperates; there is no Nash equilibrium in mixed strategies).

Appendix: Cooperative programmes

Public debt development and three programmes

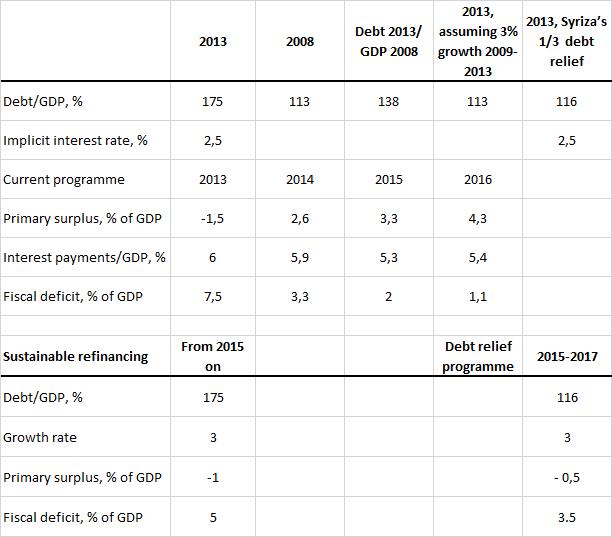
Debt to GDP ratio increased mainly due to the collapse of GDP. With 3 percent nominal growth, debt to GDP would have remained in 2013 where it had been in 2008 (it would have been 20 percentage points higher, 2013/2008 with no growth). If debt relief is one third of the current debt, debt to GDP ratio will be just slightly higher than in 2008 (116 rather than 113).

The differences between the three possible programmes of debt sustainability and pay back schedules are in the amount of primary surpluses needed. Common assumptions are: 3 percent growth rate and 2.5 percent interest rate on the total debt. (Primary surpluses are calculated from a simplified formula s = (r-g)*D, where s is the primary surplus, r is the implicit interest rate, g is the growth rate and D is debt to GDP).

If debt to GDP ratio is to remain sustainable at 175 percent, primary deficit of at most around 1 percent of GDP is needed (and fiscal deficit of around 5 percent of GDP), while primary deficit of around 0.5 percent of GDP (and fiscal deficit of around 3.5 percent) is needed to stabilise debt to GDP ratio at 116 percent. The current programme envisages significant primary surpluses, of around 4 percent of GDP, for as long as is needed to bring down debt to below 60 percent of GDP.

So, the agreement should be reached on

• whether debt relief was needed, though the difference between that programme and the one without it is not large, at least when it comes to the minimal level of primary surpluses needed for sustainability,

and then, and more importantly, on

• the time schedule of repayments, which is to say on the size of the fiscal surpluses, say between – 1 and 4 percent of GDP.

Of course, either debt would decline faster or surpluses needed would be smaller if growth accelerated beyond 3 percent, which could also be included in the repayment programme¹.

¹Comments by J. Grübler and S. Jokubauskaite are greatly appreciated. All mistakes are mine.